摘要
Python数学模型手记-(1)NetworkX 图的实际操作 1、NetworkX 图论与互联网工具箱NetworkX 是根据 Python 语言表达的图论与社会网络工具箱,用以建立、实际操作和科学研究社会网络的构造、动力学模型和作用。NetworkX 能够 以规范和非标的数据类型叙述图与互联网,转化成图与互联网,剖析网络架构,搭建网络模型,设计方案互联网优化算法,制作互联网图型。Networ…
正文
Python数学模型手记-(1)NetworkX 图的实际操作
1、NetworkX 图论与互联网工具箱
NetworkX 是根据 Python 语言表达的图论与社会网络工具箱,用以建立、实际操作和科学研究社会网络的构造、动力学模型和作用。
NetworkX 能够 以规范和非标的数据类型叙述图与互联网,转化成图与互联网,剖析网络架构,搭建网络模型,设计方案互联网优化算法,制作互联网图型。
NetworkX 给予了图型的类、目标、图型制作器、互联网制作器、制图工具,内嵌了常见的图论和聚类分析优化算法,能够 开展图和互联网的模型、剖析和模拟仿真。
NetworkX 的官方网站和文本文档
官方网站详细地址:https://networkx.org/
官方网文本文档: https://networkx.org/documentation/stable/
pdf 文本文档: https://networkx.org/documentation/stable/_downloads/networkx_reference.pdf
NetworkX 的安裝
NetworkX 的安裝规定:Python 3.2 之上版本号,强烈推荐安裝 NumPy、SciPy、Matplotlib、Graphviz 工具箱的适用。
pip 安裝:
pip3 install networkx
pip3 install networkx -i https://mirrors.aliyun.com/pypi/simple

本系列产品创作方案
NetworkX 的作用十分强劲和繁杂,所涉及到內容远远地、远远超过了数学模型的范畴,甚至是花了很长期还不可以对其开展较为系统软件的归纳。
本系列产品以数学模型学习培训和运用的要求为主导线,详细介绍有关的基本要素和典型性优化算法的运用。
=== 关心 Youcans 原創系列产品(https://www.cnblogs.com/youcans/)
2、图、端点和边的建立与操作过程
图由端点和联接端点的边组成,但与端点的部位、边的直曲长度不相干。
图给予了一种解决关联和互动等抽象化的更强的方式 ,它还给予了形象化的视觉效果方法来思索这种定义。
Networkx适用建立简易无向图、有向图和多种图(multigraph);内嵌很多规范的图论算法,连接点能为随意数据信息;适用随意的边值层面,功能丰富,简易实用。
2.1 图的基本要素
- 图(Graph)。若干点和一些联接这种点的联线,所组成关联构造便是一个图。
- 端点(Node)和边(Edge)。图上的点称之为端点,也称连接点。2个端点中间的联线,称之为边。
- 平行面边(Parallel edge)和循环系统(Cycle)。起始点同样、终点站也同样的两根边称之为平行面边。起始点和终点站重叠的边称之为循环系统。
- 有向图(Digraph)和无向图(Undirected graph)。图上的一条边都含有方位,称之为有向图;图上的一条边也没有方位,称之为无向图;有的边含有方位,有的边沒有方位,称之为混和图。
- 增权图(Weighted graph)。图上的一条边都是有一个或好几个相匹配的主要参数,称之为增权图。该主要参数称之为这条边的权,权能够 用于表明二点间的间距、時间、花费。
- 度(Degree)。与端点相接的边的总数,称之为该端点的度。
2.2 图、端点和边的实际操作
Networkx非常容易建立图、向图上加上端点和边、从图上删掉端点和边,还可以查询、删掉端点和边的特性。
图的建立
Graph()类、DiGraph()类、MultiGraph()类和MultiDiGraph() 类各自用于建立 无向图、有向图、图组和有向图组。
class Graph(incoming_graph_data=None, **attr)
import networkx as nx
import networkx as nx # 导进 NetworkX 工具箱
# 建立 图
G1 = nx.Graph() # 建立:空的 无向图
G2 = nx.DiGraph() #建立:空的 有向图
G3 = nx.MultiGraph() #建立:空的 图组
G4 = nx.MultiDiGraph() #建立:空的 有向图组
端点的加上、删掉和查询
图的每一个端点都是有唯一的标识特性(label),可以用整数金额或标识符种类表明,端点还能够自定随意特性。
端点的常见实际操作:加上端点,删掉端点,界定端点特性,查询端点和端点特性。
# 端点(node)的实际操作
G1.add_node(1) # 向 G1 加上端点 1
G1.add_node(1,name='n1',weight=1.0) # 加上端点 1,界定 name, weight 特性
G1.add_node(2,date='May-16') # 加上端点 2,界定 time 特性
G1.add_nodes_from([3, 0, 6], dist=1) # 加上好几个端点:3,0,6
# 查询端点和端点特性
print(G1.nodes()) # 查询端点
# [1, 2, 3, 0, 6]
print(G1._node) # 查询端点特性
# {1: {'name': 'n1', 'weight': 1.0}, 2: {'date': 'May-16'}, 3: {'dist': 1}, 0: {'dist': 1}, 6: {'dist': 1}}
H = nx.path_graph(8) # 建立 途径图 H:由 n个连接点、n-1条边联接,连接点标识为 0 至 n-1
G1.add_nodes_from(H) # 由途径图 H 向图 G1 加上端点 0~9
print(G1.nodes()) # 查询端点
# [1, 2, 3, 0, 6, 4, 5, 7] # 端点目录
G1.add_nodes_from(range(10, 15)) # 向图 G1 加上端点 10~14
print(G1.nodes()) # 查询端点
# [1, 2, 3, 0, 6, 4, 5, 7, 10, 11, 12, 13, 14]
# 从图上删掉端点
G1.remove_nodes_from([1, 11, 13, 14]) # 根据端点标识的 list 删掉好几个端点
print(G1.nodes()) # 查询端点
# [2, 3, 0, 6, 4, 5, 7, 10, 12] # 端点目录
# === 关心 Youcans 原創系列产品(https://www.cnblogs.com/youcans/)
边的加上、删掉和查询
边是2个端点中间的联接,在 NetworkX 选用 边是由相匹配端点的名称的元组构成 e=(node1,node2)。边能够 设定权重值、关联等特性。
边的常见实际操作:加上边,删掉边,界定边的特性,查询边和边的特性。向图上加上边时,假如加上的边的端点是图上不会有的,则全自动向图上加上该端点。
# 边(edge)的实际操作
G1.add_edge(1,5) # 向 G1 加上边 1-5,并全自动加上图上沒有的端点
G1.add_edge(0,10, weight=2.7) # 向 G1 加上边 0-10,并设定特性
G1.add_edges_from([(1,2,{'weight':0}), (2,3,{'color':'blue'})]) # 向图上加上边,并设定特性
print(G1.nodes()) # 查询端点
# [2, 3, 0, 6, 4, 5, 7, 10, 12, 1] # 全自动加上了图上沒有的端点 1
G1.add_edges_from([(3,6),(1,2),(6,7),(5,10),(0,1)]) # 向图上加上好几条边
G1.add_weighted_edges_from([(1,2,3.6),[6,12,0.5]]) # 向图上加上好几条增权边: (node1,node2,weight)
G1.remove_edge(0,1) # 从图上删掉边 0-1
# G1.remove_edges_from([(2,3),(1,5),(6,7)]) # 从图上删掉好几条边
# print(G1.edges(data=True)) # 查询全部边的特性
print(G1.edges) # 查询全部边
# [(2, 1), (2, 3), (3, 6), (0, 10), (6, 7), (6, 12), (5, 1), (5, 10)]
print(G1.get_edge_data(1,2)) # 查询特定边 1-2 的特性
# {'weight': 3.6}
print(G1[1][2]) # 查询特定边 1-2 的特性
# {'weight': 3.6}
查询图、端点和边的信息内容
print(G1.nodes) # 回到全部的端点 [node1,...]
# [1, 2, 0, 6, 4, 12, 5, 9, 8, 3, 7]
print(G1.edges) # 回到全部的边 [(node1,node2),...]
# [(1,5), (1,2), (2,8), (2,3), (0,9), (6,5), (6,7), (6,12), (4,3), (4,5), (9,8), (8,7)]
print(G1.degree) # 回到各端点的度 [(node1,degree1),...]
# [(1,2), (2,3), (0,1), (6,3), (4,2), (12,1), (5,3), (9,2), (8,3), (3,2), (7,2)]
print(G1.number_of_nodes()) # 回到全部的端点 [node1,...]
# 11
print(G1.number_of_edges()) # 回到全部的端点 [node1,...]
# 12
print(G1[2]) # 回到特定端点邻近的端点和端点的特性
# {1: {'weight': 3.6}, 8: {'color': 'blue'}, 3: {}}
print(G1.adj[2]) # 回到特定端点邻近的端点和端点的特性
# {1: {'weight': 3.6}, 8: {'color': 'blue'}, 3: {}}
print(G1[6][12]) # 回到特定边的特性
# {'weight': 0.5}
print(G1.adj[6][12]) # 回到特定边的特性
# {'weight': 0.5}
print(G1.degree(5)) # 回到特定端点的度
# 3
print('nx.info:',nx.info(G1)) # 回到图的基本资料
print('nx.degree:',nx.degree(G1)) # 回到图上各端点的度
print('nx.density:',nx.degree_histogram(G1)) # 回到图轻中度的遍布
print('nx.pagerank:',nx.pagerank(G1)) # 回到图上各端点的頻率遍布
2.3 图的特性和方式
图的方式
| 方式 | 表明 |
|---|---|
| G.has_node(n) | 当图 G 中包含端点 n 时回到 True |
| G.has_edge(u, v) | 当图 G 中包含边 (u,v) 时回到 True |
| G.number_of_nodes() | 回到 图 G 中的端点的总数 |
| G.number_of_edges() | 回到 图 G 中的边的总数 |
| G.number_of_selfloops() | 回到 图 G 中的自循环系统边的总数 |
| G.degree([nbunch, weight]) | 回到 图 G 中的所有端点或特定端点的度 |
| G.selfloop_edges([data, default]) | 回到 图 G 中的所有的自循环系统边 |
| G.subgraph([nodes]) | 从图 G1中提取端点[nodes]及相匹配边组成的子图 |
| union(G1,G2) | 合拼图 G1、G2 |
| nx.info(G) | 回到图的基本资料 |
| nx.degree(G) | 回到图上各端点的度 |
| nx.degree_histogram(G) | 回到图轻中度的遍布 |
| nx.pagerank(G) | 回到图上各端点的頻率遍布 |
| nx.add_star(G,[nodes],**attr) | 向图 G 加上星型互联网 |
| nx.add_path(G,[nodes],**attr) | 向图 G 加上一条途径 |
| nx.add_cycle(G,[nodes],**attr) | 向图 G 加上合闭途径 |
方法:
# Copyright 2021 YouCans, XUPT
G1.clear() # 清除图G1
nx.add_star(G1, [1, 2, 3, 4, 5], weight=1) # 加上星型互联网:以第一个端点为管理中心
# [(1, 2), (1, 3), (1, 4), (1, 5)]
nx.add_path(G1, [5, 6, 8, 9, 10], weight=2) # 加上途径:次序联接 n个连接点的 n-1条边
# [(5, 6), (6, 8), (8, 9), (9, 10)]
nx.add_cycle(G1, [7, 8, 9, 10, 12], weight=3) # 加上闭合回路:循环系统联接 n个连接点的 n 条边
# [(7, 8), (7, 12), (8, 9), (9, 10), (10, 12)]
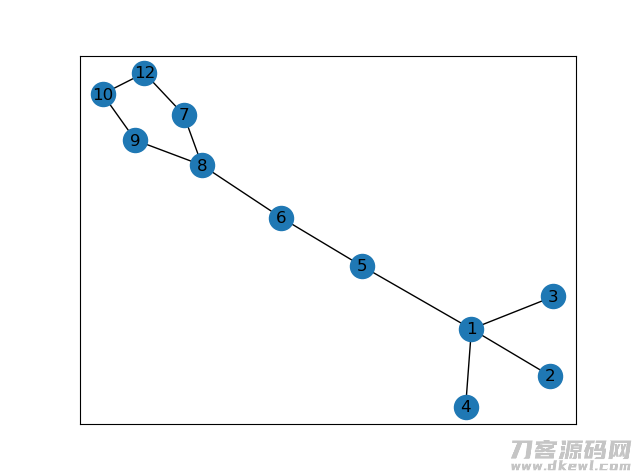
print(G1.nodes) # 回到全部的端点 [node1,...]
nx.draw_networkx(G1)
plt.show()
G2 = G1.subgraph([1, 2, 3, 8, 9, 10])
G3 = G1.subgraph([4, 5, 6, 7])
G = nx.union(G2, G3)
print(G.nodes) # 回到全部的端点 [node1,...]
# [1, 2, 3, 8, 9, 10, 4, 5, 6, 7]
3、图的制作与剖析
3.1 图的制作
数据可视化是图论和网络问题中很重要的內容。NetworkX 在 Matplotlib、Graphviz 等图型工具箱的基本上,给予了丰富多彩的制图作用。
本系列产品拟对图和互联网的数据可视化作一个专题讲座,在这里只简易详细介绍根据 Matplotlib 的基本上制图涵数。基本上制图涵数应用词典给予的部位将连接点置放在散点图上,或是应用合理布局函数计算部位。
| 方式 | 表明 |
|---|---|
| draw(G[,pos,ax]) | 根据 Matplotlib 制作 图 G |
| draw_networkx(G[, pos, arrows, with_labels]) | 根据 Matplotlib 制作 图 G |
| draw_networkx_nodes(G, pos[, nodelist, . . . ]) | 绘制图 G 的端点 |
| draw_networkx_edges(G, pos[, edgelist, . . . ]) | 绘制图 G 的边 |
| draw_networkx_labels(G, pos[, labels, . . . ]) | 制作端点的标识 |
| draw_networkx_edge_labels(G, pos[, . . . ]) | 制作边的标识 |
在其中,nx.draw() 和 nx.draw_networkx() 是最基本上的制图涵数,并能够 根据自定义函数特性或其他制图涵数设定不一样的制图规定。常见的特性界定以下:
- ‘node_size’:特定连接点的规格尺寸,默认设置300
- ‘node_color’:特定连接点的色调,默认设置鲜红色
- ‘node_shape’:连接点的样子,默认设置环形
- ”alpha’:清晰度,默认设置1.0,不全透明
- ‘width’:边的总宽,默认设置1.0
- ‘edge_color’:边的色调,默认设置灰黑色
- ‘style’:边的款式,可选 ‘solid’、’dashed’、’dotted’、’dashdot’
- ‘with_labels’:连接点是不是带标识,默认设置True
- ‘font_size’:连接点标识文字大小,默认设置12
- ‘font_color’:连接点标识字体样式,默认设置灰黑色
3.2 图的剖析
NetwotkX 给予了图论涵数对图的构造开展剖析:
子图
子图就是指端点和边都分别是图 G 的端点的非空子集和边的非空子集的图。
subgraph()方式 ,按端点从图 G 中抽出来子图。方法如前。
连接子图
假如图 G 中的随意二点间互相连接,则 G 是连通图。
connected_components()方式 ,回到连接子图的结合。
G = nx.path_graph(4)
nx.add_path(G, [7, 8, 9])
# 连接子图
listCC = [len(c) for c in sorted(nx.connected_components(G), key=len, reverse=True)]
maxCC = max(nx.connected_components(G), key=len)
print('Connected components:{}'.format(listCC)) # 全部连接子图
# Connected components:[4, 3]
print('Largest connected components:{}'.format(maxCC)) # 较大连接子图
# Largest connected components:{0, 1, 2, 3}
** 强连接**
假如有向图 G 中的随意二点间互相连接,则称 G 是强连通图。
strongly_connected_components()方式 ,回到全部强连接子图的目录。
# 强连接
G = nx.path_graph(4, create_using=nx.DiGraph())
nx.add_path(G, [3, 8, 1])
# 找到全部的强连接子图
con = nx.strongly_connected_components(G)
print(type(con),list(con))
# <class 'generator'> [{8, 1, 2, 3}, {0}]
弱连接
假如一个有向图 G 的基图是连通图,则有向图 G 是弱连通图。
weakly_connected_components()方式 ,回到全部弱连接子图的目录。
# 弱连接
G = nx.path_graph(4, create_using=nx.DiGraph()) #默认设置转化成连接点 0,1,2,3 和有向边 0->1,1->2,2->3
nx.add_path(G, [7, 8, 3]) #转化成有向边:7->8->3
con = nx.weakly_connected_components(G)
print(type(con),list(con))
# <class 'generator'> [{0, 1, 2, 3, 7, 8}]
=== 关心 Youcans 原創系列产品(https://www.cnblogs.com/youcans/)
著作权表明:
论文参考文献申明:文中一部分內容参照了 NetworkX 官方网站详细介绍:https://networkx.org/documentation/stable/
YouCans 原创作品
Copyright 2021 YouCans, XUPT
Crated:2021-05-16
关注不迷路
扫码下方二维码,关注宇凡盒子公众号,免费获取最新技术内幕!






评论0