放射线与室内空间内三角形的交叉检验优化算法（Möller-Trumbore）的计算与实践活动

情况详细介绍(学习培训优化算法以前必须先掌握)

放射线与室内空间内三角形的交叉检验是游戏编程设计中一个普遍的难题，最典型性的运用便是捡取(Picking)，文中详细介绍一个最普遍的方式，这一方式也是DirectX中选用的方式，该方式速度更快，并且储存空间少。先叙述基础理论，随后文章内容结尾得出相匹配的编码完成与Unity中的表明。
简易而形象化的方式是：先分辨放射线是不是与三角形所属的平面图交叉，假如交叉，再分辨相交点是不是在三角形内。但这类方式高效率并不高，由于多测算了三角形所属的平面图。
Möller-Trumbore放射线三角交叉优化算法是一种迅速测算放射线与室内空间内三角形的相交点的方式，根据空间向量与矩阵运算能够迅速得到相交点与重心坐标，而不用对包括三角形的平面方程开展预估算。它运用于电子计算机图象处理中以完成涉及到三角形网格图的光源追踪测算。优化算法名称是以发明人TomasMöller和Ben Trumbore的名称来取名的。

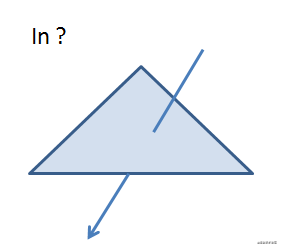
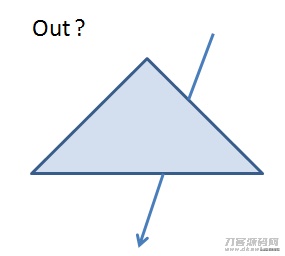
主要参数表明

设放射线的方程组Ray=O td(O为起始点，D为放射线方位(方向向量)，t为权重值)，一个点从起始点O逐渐，顺着方位D挪动随意长短，获得终点站R，依据t值得不一样，获得得R值也不一样，全部这种不一样的R值便组成了成条放射线。
三角形三个端点P0，P1，P2。u为P1的权重值，v为P2的权重值，而1-u-v是P0的权重值，能够了解为顺着边AC挪动一段距离，随后再顺着边AB挪动一段距离，最终求他们的和空间向量。对于挪动多少间距，便是由主要参数u和v操纵的，所表述的数学课实际意义是三角形以及內部全部点的方程组。

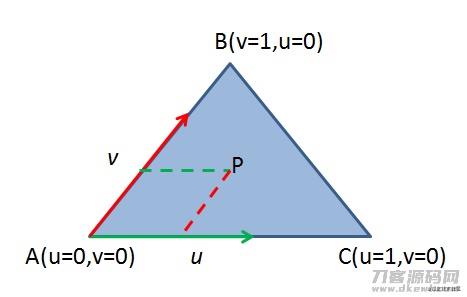
\[Ray:O td{\quad}(t≥0)
\]

\[(1-u-v)P0 uP1 vP2
\]

计算全过程

2个关键的定律

克莱姆法则

解线性微分方程时

\[\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]\left[ \begin{matrix} t \\ u \\ v\end{matrix} \right]=S
\]

D，E1，E2是带有三个主要参数的行列式，就可以表述成

\[ t=\frac{det{\left[ \begin{matrix} S & E_1 & E_2\end{matrix} \right]}}{det{\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]}}=\frac{\left[ \begin{matrix} S_x & E_{x1} & E_{x2} \\ S_y & E_{y1} & E_{y2} \\ S_{z} & E_{z1} & E_{z2}\end{matrix} \right]}{\left[ \begin{matrix} -D_x & E_{x1} & E_{x2} \\ -D_y & E_{y1} & E_{y2} \\ -D_{z} & E_{z1} & E_{z2}\end{matrix} \right]}
\]

\[ u=\frac{det{\left[ \begin{matrix} -D & S & E_2\end{matrix} \right]}}{det{\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]}}=\frac{\left[ \begin{matrix} -D_x & S_x & E_{x2} \\ -D_y & S_y & E_{y2} \\ -D_{z} & S_z & E_{z2}\end{matrix} \right]}{\left[ \begin{matrix} -D_x & E_{x1} & E_{x2} \\ -D_y & E_{y1} & E_{y2} \\ -D_{z} & E_{z1} & E_{z2}\end{matrix} \right]}
\]

\[ v=\frac{det{\left[ \begin{matrix} -D & E_1 & S\end{matrix} \right]}}{det{\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]}}=\frac{\left[ \begin{matrix} -D_x & E_{x1} & S_{x} \\ -D_y & E_{y1} & S_y \\ -D_{z} & E_{z1} & S_z\end{matrix} \right]}{\left[ \begin{matrix} -D_x & E_{x1} & E_{x2} \\ -D_y & E_{y1} & E_{y2} \\ -D_{z} & E_{z1} & E_{z2}\end{matrix} \right]}
\]

空间向量混合积

\[ a·(b×c)=b·(c×a)=c·(a×b)\\
a·(b×c)=-a·(c×b)\\
a·(b×c)=-b·(a×c)\\
a·(b×c)=-c·(b×a)
\]

将方程组联立

\[O td=(1-u-v)P0 P1 P2{\quad}(u≥0,v≥0,u v≤1)
\]

化简

\[O-P0=u(P1-P0) v(P2-P0)-td\\
S=uE_1 vE_2-td\\{\quad}(S=O-P0,E_1=P1-P0,E_2=P2-P0)
\]

\[\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]\left[ \begin{matrix} t \\ u \\ v\end{matrix} \right]=S
\]

安布罗规律

\[t=\frac{det{\left[ \begin{matrix} S & E_1 & E_2\end{matrix} \right]}}{det{\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]}}
\]

空间向量混合积
真分数一部分
应用空间向量混合积定律，D前的-号，被相抵了

\[ det{\left[ \begin{matrix} -D & E_1 & E_2\end{matrix} \right]}=-D·(E_1×E_2)=E_1·(D×E_2)
\]

令

\[ S1=D×E_2
\]

分子结构一部分：

\[ det{\left[ \begin{matrix} S & E_1 & E_2\end{matrix} \right]}=((S×E_1)·E_2)
\]

令

\[ S2=S×E_1
\]

原式相当于

\[ det{\left[ \begin{matrix} S & E_1 & E_2\end{matrix} \right]}=S2·E_2
\]

因而

\[ t=\frac{S2·E_2}{E_1·S1}
\]

同样可把责任推卸的别的2个主要参数u，v

\[ u=\frac{S1·S}{E_1·S1}
\]

\[ v=\frac{S2·D}{E_1·S1}
\]

汇总

我们在最终能够根据已经知道的数据信息，算出t、u、v三个主要参数，根据三个主要参数的范畴限定分辨是不是交叉，假如不符合则不交叉，假如达到则交叉

编码完成

    // Vector3 a b c triangle vertexs
    // orig is ray original point, dir is direction vector
    bool rayTriangleIntersect(Vector3 orig, Vector3 dir,
        Vector3 a, Vector3 b, Vector3 c, float t, float b1, float b2)
    {
        bool isIn = false;
        Vector3 E1 = b - a;
        Vector3 E2 = c - a;
        Vector3 S = orig - a;
        Vector3 S1 = Vector3.Cross(dir, E2);
        Vector3 S2 = Vector3.Cross(S, E1);

        // 一同指数
        float coeff = 1.0f / Vector3.Dot(S1, E1);
        t = coeff * Vector3.Dot(S2, E2);
        b1 = coeff * Vector3.Dot(S1, S);
        b2 = coeff * Vector3.Dot(S2, dir);

        Debug.Log($"t = {t}, b1 = {b1}, b2 = {b2}");

        if (t >= 0 && b1 >= 0 && b2 >= 0 && (1 - b1 - b2) >= 0)
        {
            isIn = true;
        }

        return isIn;
    }

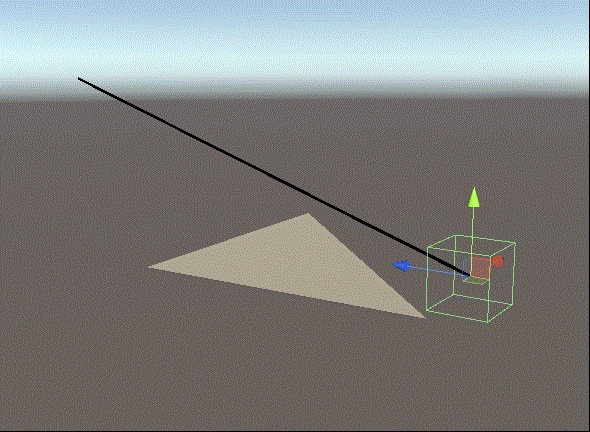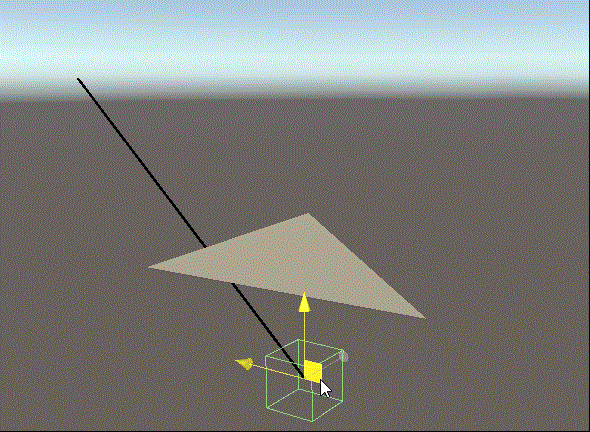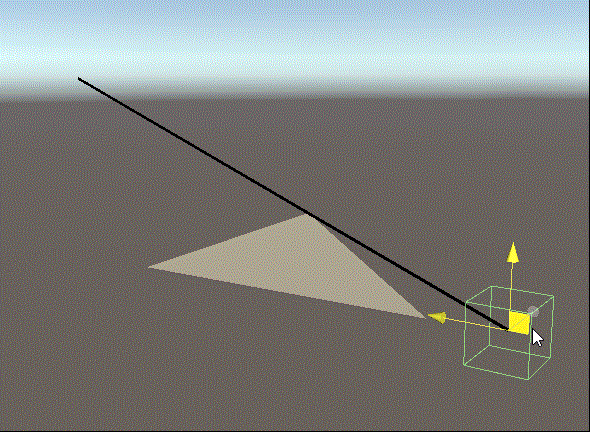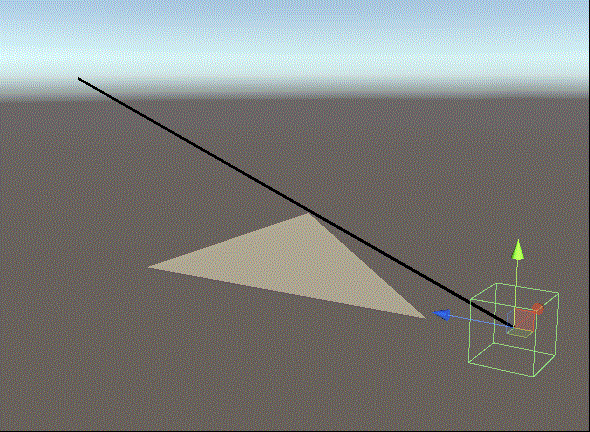
Unity中的演试实际效果

当放射线与三角形交叉时，三角形的材料会变为鲜红色，放射线是选用LineRenderer的方式，三角形用了编写材料端点的脚本制作，过几天会共享出去~
新项目详细地址:https://GitHub.com/shadow-lr/RayTriangleIntersect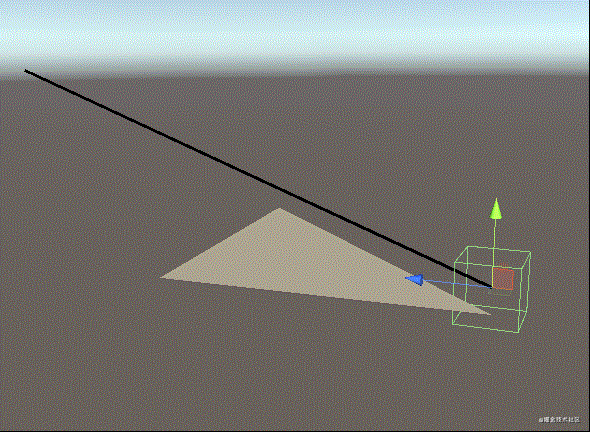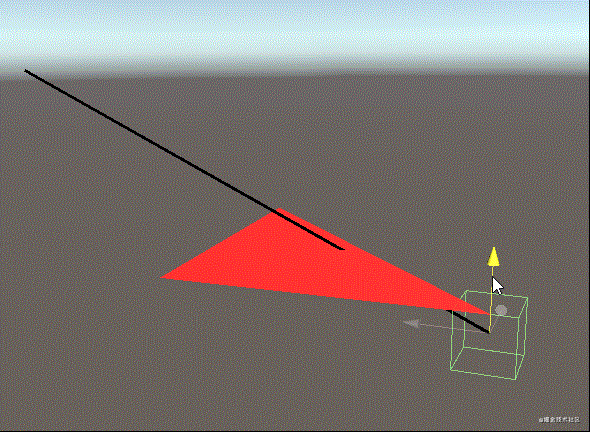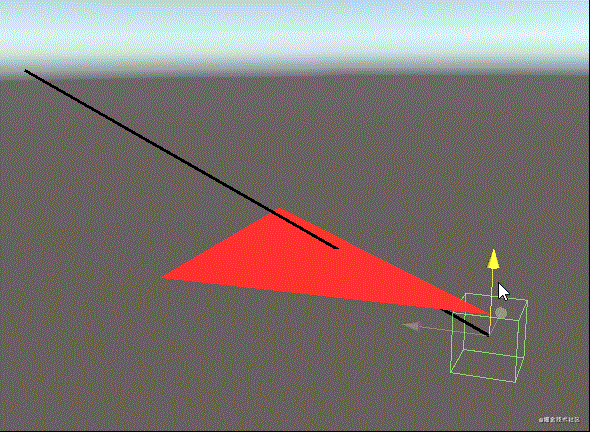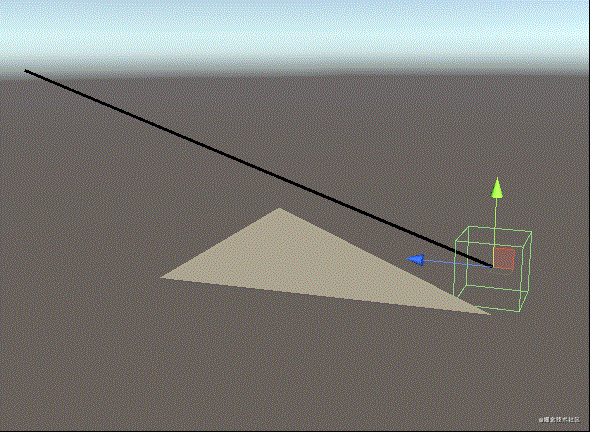

题外话

尽管放射线和三角形的交叉检验能够用于完成捡取(Picking)，可是大部分程序流程并不选用这一方式，缘故是这一方式高效率很低，我们可以构想，一个大中型的手机3d游戏，某一实体模型的三角形总数很可能是上百万级的，在这里状况下，模型拟合上的每一个三角形求交是一件极为消耗時间的事儿。
因此 一般行得通的方式是，用包围着球和包围盒（AABB、OBB、FDH）来替代，测算出能容下实体模型的最少圆球或是举办提，只需分辨放射线与包围着球或是包围盒求交就可以，仅仅精准度上面有一定差值，可是足够达到大部分程序流程的必须。