深度学习探析-回归分析

题外话

我很早已对人工智能技术是十分有兴趣的。记得我高校的论文，便是应用进化算法解决了一个經典的寻径难题。
我一直对人们經典的观念是十分敬畏之心和钦佩的，例如传统式的电子计算机算法设计优化算法难题，比如經典的排序算法或是动态规划观念，把一些看起来
繁杂的难题居然用短短的十几行乃至一个 for 循环系统就能处理，这令我体会到一种艺术美学，也另外对人们的杰出观念而赞美。
但传统式的计算机算法实际上或是根据，人来撰写编码，人来根据详细的、解决困难的构思来解决困难。但假如设备能有自身的观念，假如它自身就能“学习培训”到解决困难的方式 ，简直十分 cool 的一件事。但以我现阶段的认知能力看来，如今的人工智能技术是更好像一种专用工具，一种“数学软件”，一种“统计学专用工具”，
它是以很多数据信息里汇总出了一种“规律性”，用于处理具体难题。它离电脑上真真正正有观念还相去甚远，乃至以现阶段看来，二者很有可能并并不是一回事儿。很有可能让设备具备逻辑思维，还必须在别的课程上开展提升例如人的认知能力体制，神经科学开展提升。嘿嘿扯远了。

先来自我介绍的一些简易了解。

线形

1. 什么叫线形？

有一类几何图形目标，例如平行线、平面图、正方体，看起来全是棱角分明的，全是“直”的，在初中数学称之为线形

要解决他们有关的难题就比较简单。例如在普通高中入学过，二根平行线可以用2个线性方程来表明，去求他们相交点得话：

联立出二者的方程，算出该方程的解就可以获得相交点

2. 为何要科学研究线形

（1）大家所在的全球、宇宙空间太繁杂了，许多状况都没法了解，更算不上用数学课去叙述；

（2）有一些合乎特殊条件的繁杂难题，能够转换为简易的线形难题。线形难题就可以彻底被了解，彻底能够被数学课所叙述

重归

以我现阶段的认知能力看来，深度学习关键的每日任务有两大类。
第一便是归类每日任务，例如

• 分辨一张图片里的是猫或是狗 （二分类，由于我界定总体目标结果有二种，即猫或是狗）
• 分辨一个个股明天是涨或是跌
• 分辨一个照片中的数据是几（多归类。由于我界定总体目标结果有 10 种，0 到 9）

换句话说，归类的結果是，人为因素事先界定的結果范畴里的一种

而第二类每日任务便是重归每日任务，而它得到的結果是一个持续数据的值，并非类型。
比如

• 预测分析房子价钱
• 预测分析股价

什么叫深度学习

这是我现阶段的粗浅了解。深度学习现阶段我认为是一种数学软件。根据来养设备很多的学习材料，随后设备运转一个深度学习优化算法，训炼出了一个实体模型。随后再向设备丢进难题，设备根据这一实体模型计算得到結果。

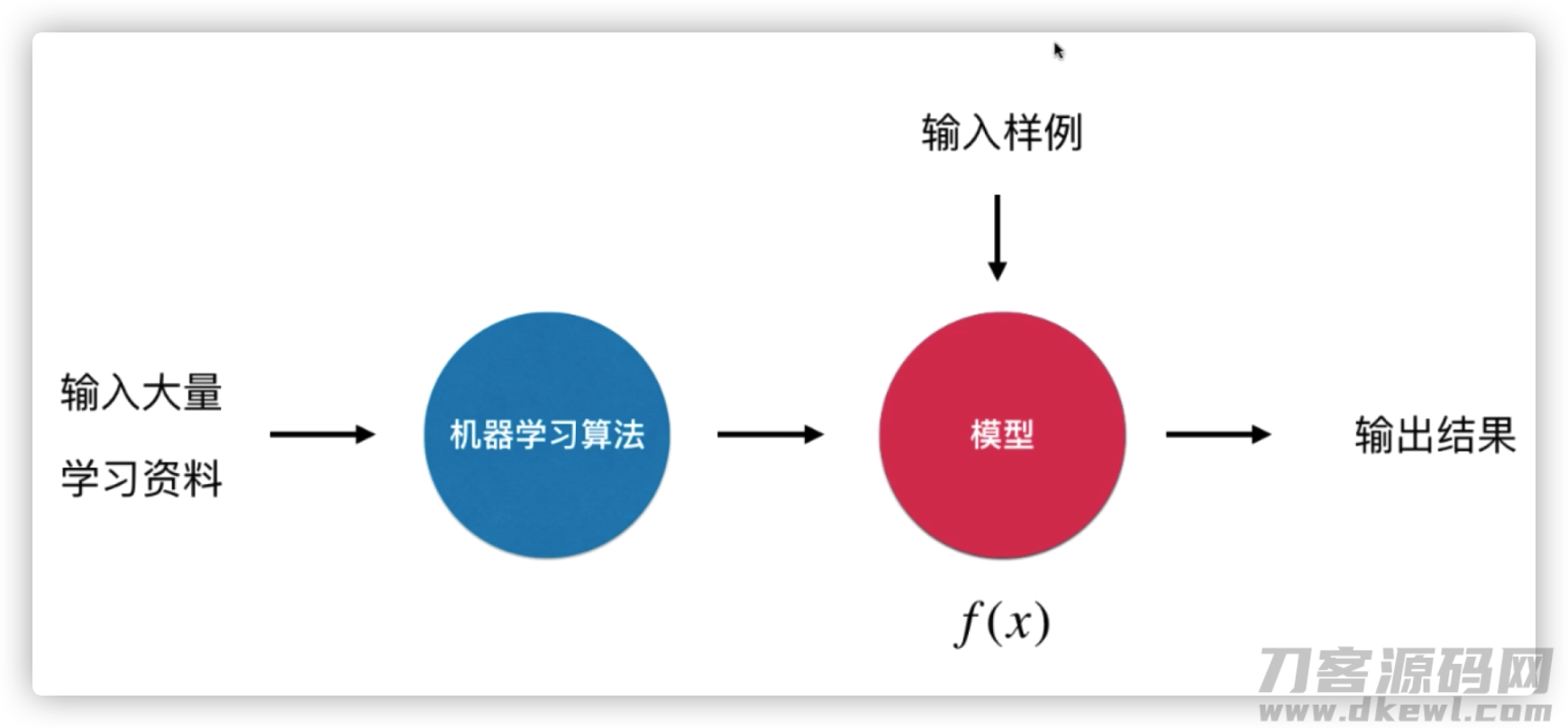
回归分析的基本理性了解

例如我搜集到有 x, y 的2组数据信息（例如年纪和个子），我要了解这2组自变量是不是有线性相关。那麼我先以一个自变量为 x 轴，另一个自变量为 y 轴绘制那样一副散点图。

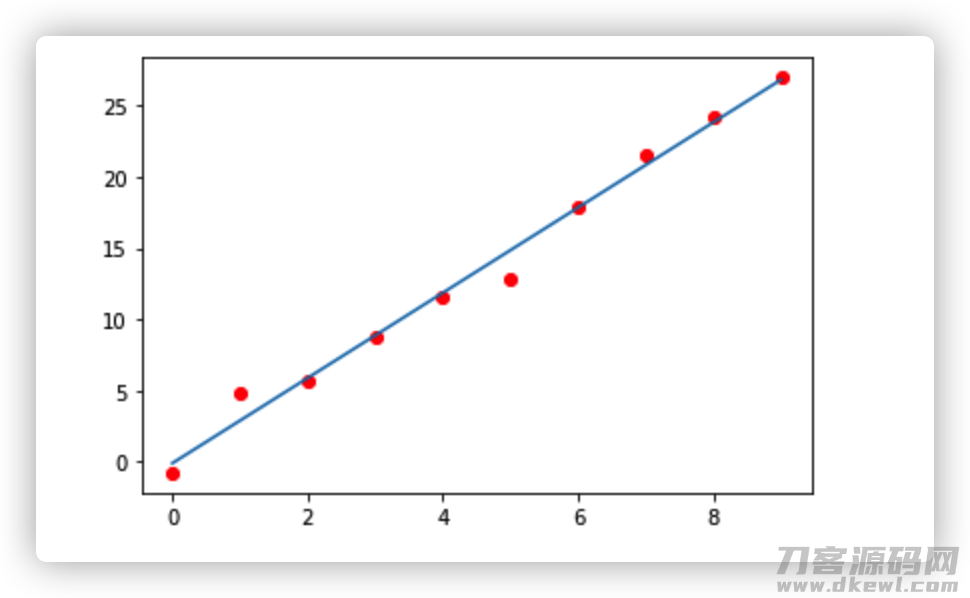
那麼我也能够找到那样的一条平行线。这条平行线的特点是：尽量的离全部离散变量点近期，还可以描述成，每一个离散变量点离直线距离的误差之和最少。
那麼我也能够非常好的依据我计算的这一条平行线，由已经知道的 x 值，来预测分析的不明的 y 值。
倘若说 x, y 有线性相关得话，那麼预测分析的实际效果或是很非常好的。因此回归分析的关键每日任务是，找到这条平行线。

单自变量回归分析

大家先从单自变量回归分析逐渐了解，即假定 x 只有一个特点（例如一氧化氮浓度值），y 是房子价格。
依据前文提及的理性了解，大家的总体目标便是寻找最好的直线方程：

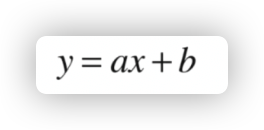
实际上便是求主要参数 a 和 b 的全过程。
那实际上大家的总体目标便是，促使依据每一个 x 点,促使

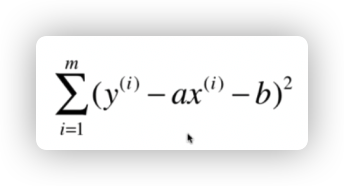
最少。这一方程组称为损失函数。
你很有可能想问为什么是差的平均数最少？而不是差的平方根和最少或是差的 3 或是 4 三次方最少？
差的平均数最少在初中数学称为最小二乘法，这儿得出一个连接
https://www.zhihu.com/question/24095027，这儿不会再深究。

因此一类深度学习优化算法的理论依据是： 根据明确难题的损失函数，随后最优控制损失函数，来得到深度学习的实体模型。
如何求取这一损失函数的极小值，即求 a 和 b 的值。则必须对 a 和 b 各自开展求导。导函数为 0 的点则为极值点。
如今大家对 a 开展求导(复合函数的链条式求导法则)：

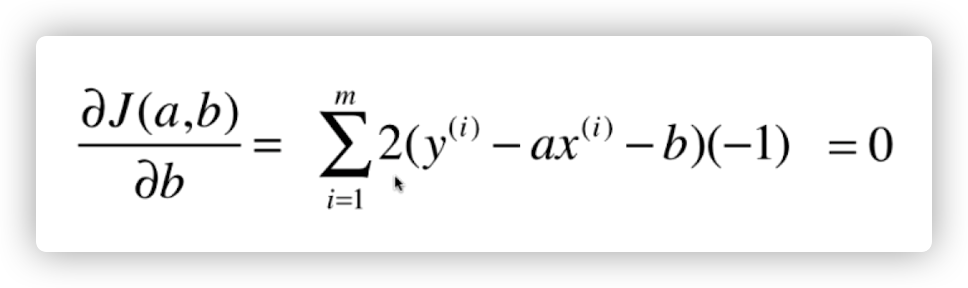
化简一下：

依据一样的全过程得到 a,化简全过程省去：

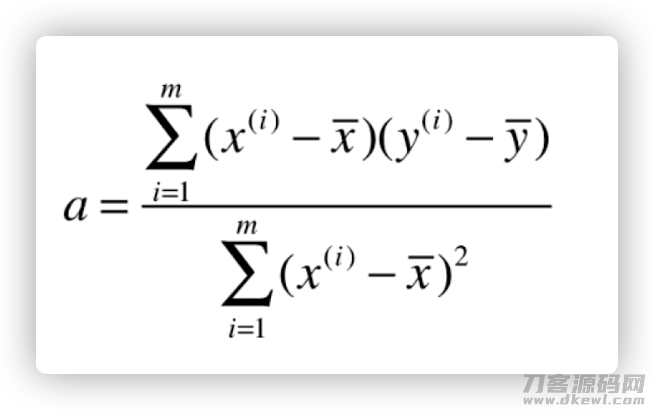
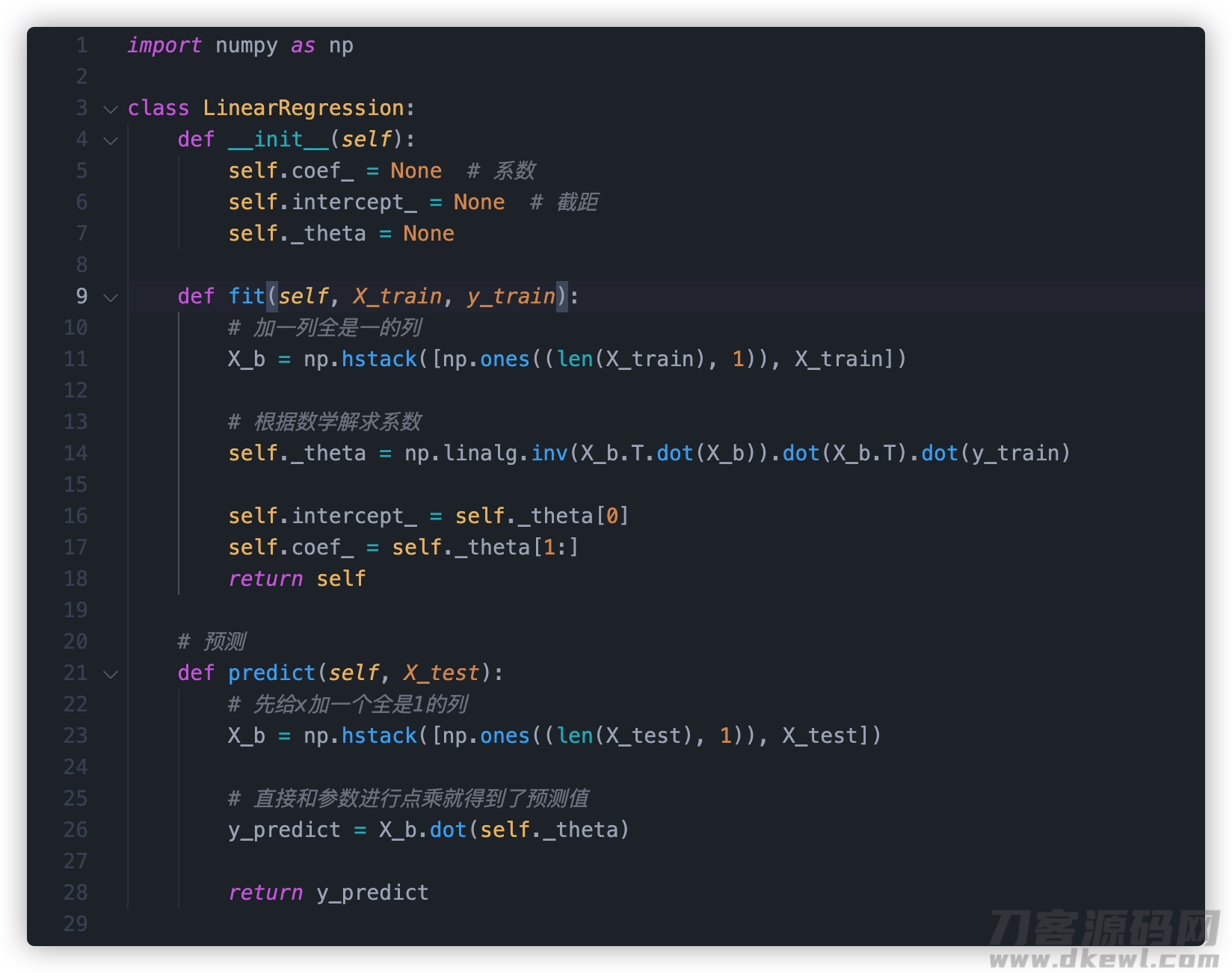
随后 python 完成一下：
简易而言我需要界定2个方式 。

• fit 线性拟合方式 。或是大家常说的训练法。根据将训炼数据信息做为主要参数传到这一方式 ，得到实体模型的每个主要参数。
• predict 预测分析方式 。将 x 值带到这一方式 ，得到估计值

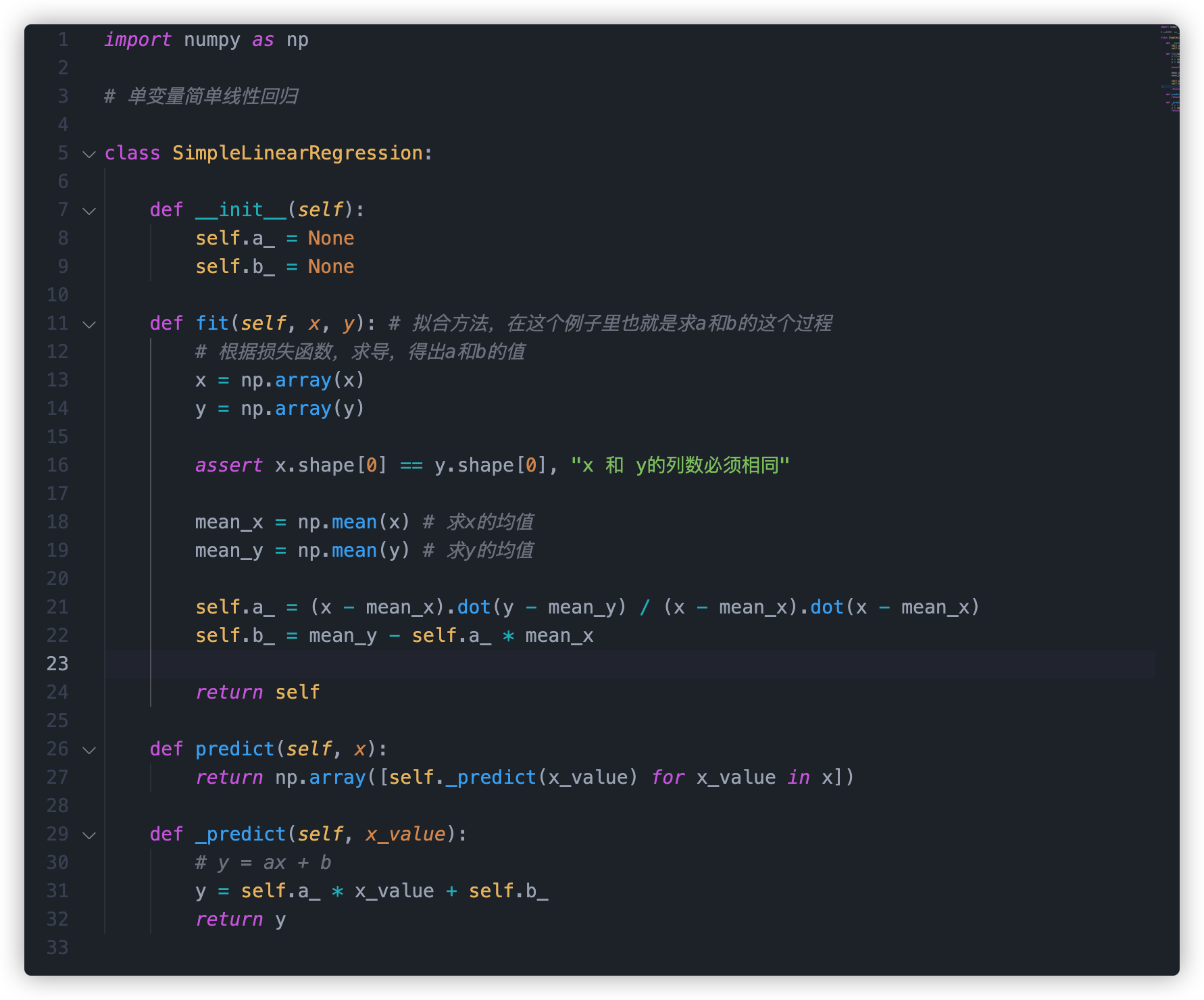
这儿必须留意一下：这儿选用了向量化分析替代了循环系统去求 a。 大家见到，a 的分子分母事实上用循环系统还可以求，
可是事实上，a 的分子分母实际上能够当做向量的点乘（即空间向量 a 里的每一个份量乘于空间向量 b 里的每一个份量）。
那样做有两个益处：

• 编码更清楚
• 空间向量是并行处理计算。（启用 GPU 流处理器开展并行处理计算）远快于 cpu 里开展循环系统

当把这个 a 和 b 的主要参数求出以后，大家就得到了一个实体模型（在这个事例中是 y=ax b），随后大家就可以开展预测分析了，把 x 带到这一方程组中，就可以得到预测分析后的这一 y 值。

多元化回归分析

了解了单自变量回归分析以后，大家就逐渐必须处理，当特点为好几个的情况下，如何开展预测分析？
也就是多元化回归分析。
我们可以了解一下，多元化回归分析具体规定的是那样的一个方程组

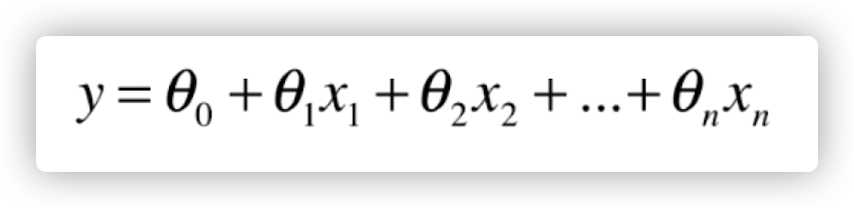
即每一个特点前边都是有一个参量指数，再加一个参量（截距）。
这儿大家把这种指数梳理成一个（列）空间向量

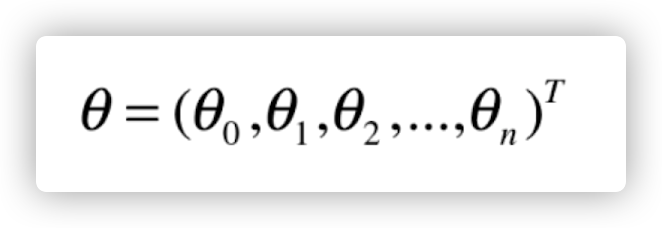
随后大家为了更好地便捷考虑，设定一个 x0, x0 恒等于 1，那麼大家最后就化简变成下边2个向量的点乘

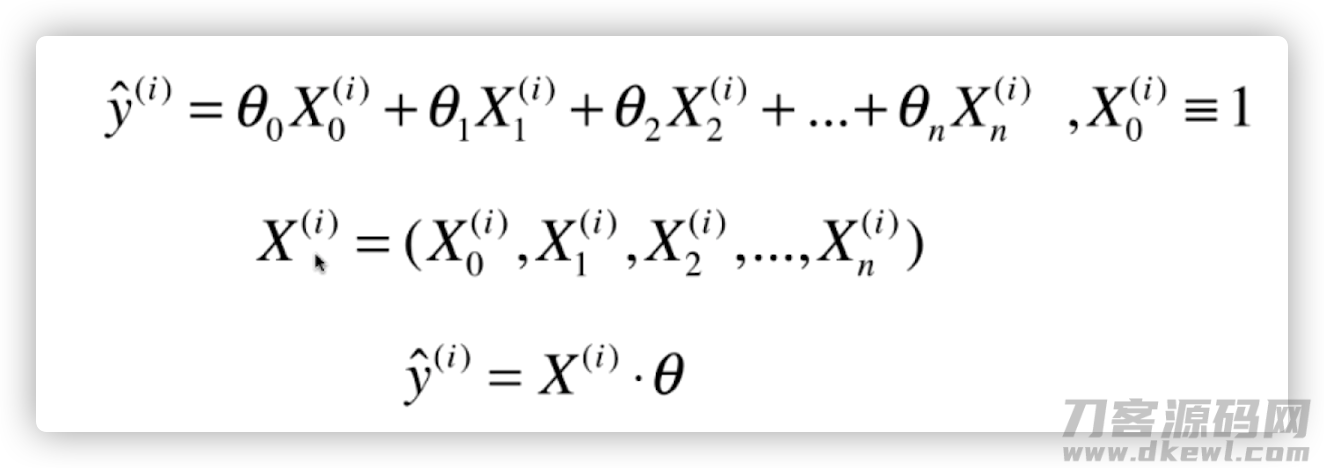
随后把全部的 x 空间向量（样版）组成一个引流矩阵，将 theta 梳理成一个列向量。那麼 y(空间向量)便是全部 x 空间向量的估计值。这儿采用了引流矩阵和向量的乘法（嘿嘿忘记了得话得备考一下离散数学）。

那麼依据最小二乘法，大家的总体目标便是促使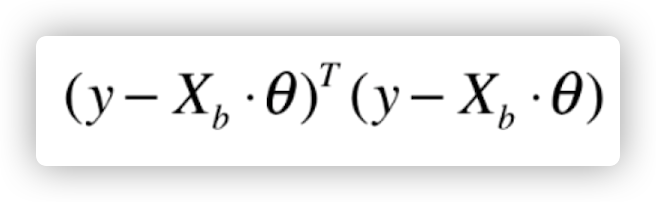

最少。也就是要对全部引流矩阵开展求导，实际计算全过程省去，这儿得出最后 theta 的解：

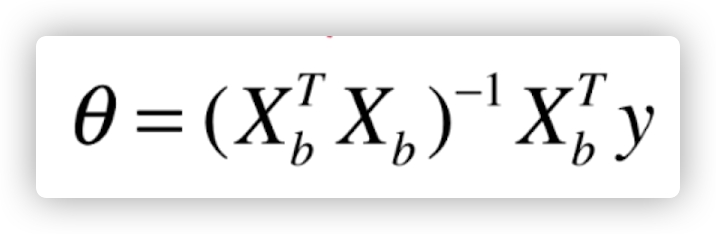
也就是大家根据数学课计算，立即求出了主要参数的数学课解，殊不知一般而言，可以立即得到主要参数数学课解的深度学习方式 或是较为少的，有可能还必须依靠别的方式 例如梯度下降法才可以求出主要参数。

多元化回归分析的完成

下面依据这一数学课解开展完成。

简易回归分析实战演练（波士顿房价预测分析）

这一波士顿房价数据是 sklearn(一个深度学习架构)内置的数据

实际上我看到这一数据时也愣住，这一事例是带大家预测分析房子价格吗？预测分析明日深圳的房价？
我认为是能够那样了解，根据搜集一些特点（学习材料）如下图和墨尔本一些地域的平均房价（总体目标结果），来推断出你或是房地产开发商卖房时应当如何标价较为划得来。换句话说根据这一数据来了解，哪一个要素针对房子价格危害更高。

数据信息详细介绍

该数据包括密苏里州墨尔本近郊区的房源信息数据信息，来源于 UCI 深度学习知识库系统（数据已退出），于 1978 年逐渐统计分析，包含 506 个样版，每一个样版包含 12 个特点自变量和该地域的平均房价。

字段名含意

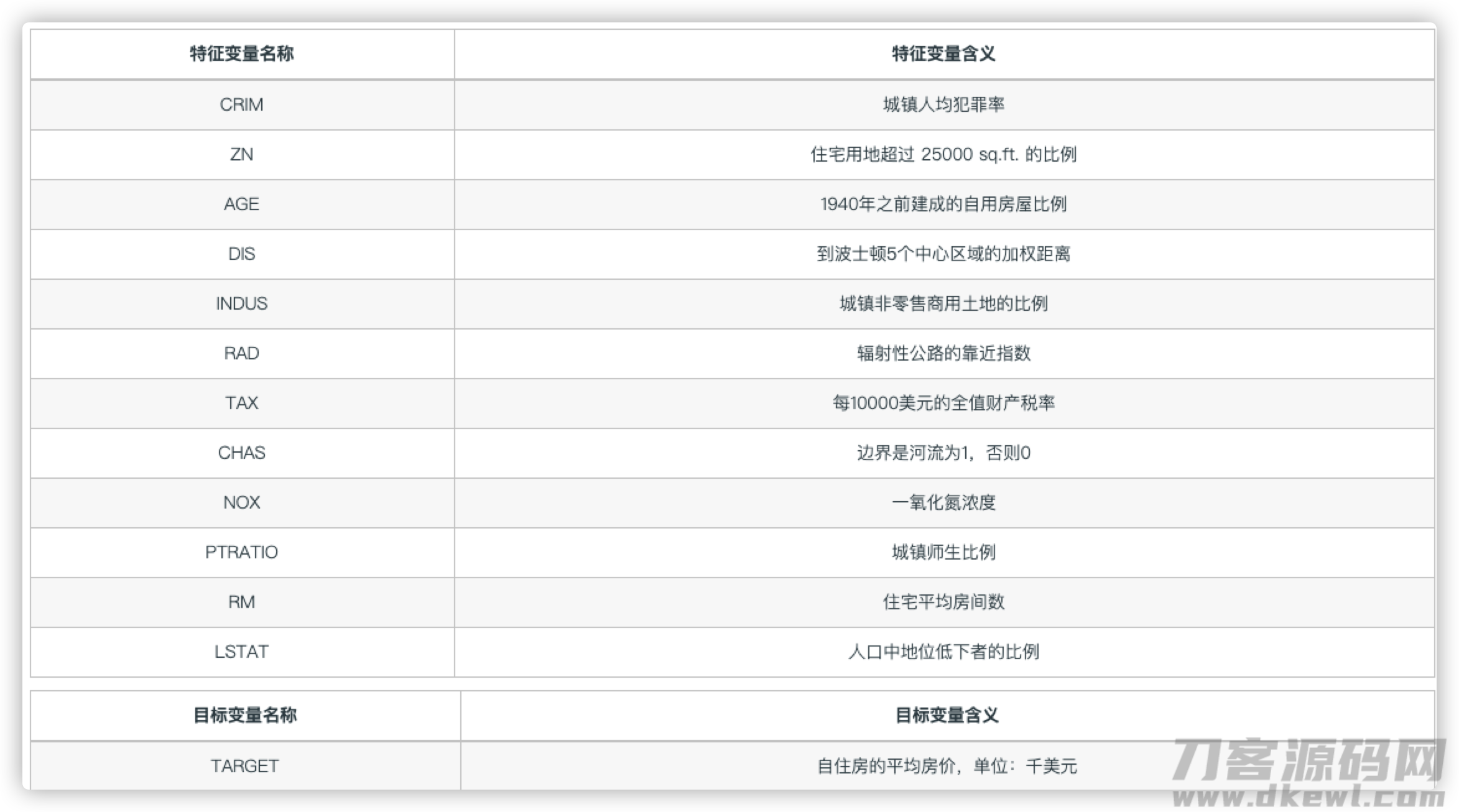
能够见到，学者期待找到危害房子价格的关键要素，例如环境要素（一氧化氮浓度值），部位要素（到墨尔本 5 个管理中心地区的权重计算间距）这些（但是相信危害中国楼市要素要比这繁杂的多）

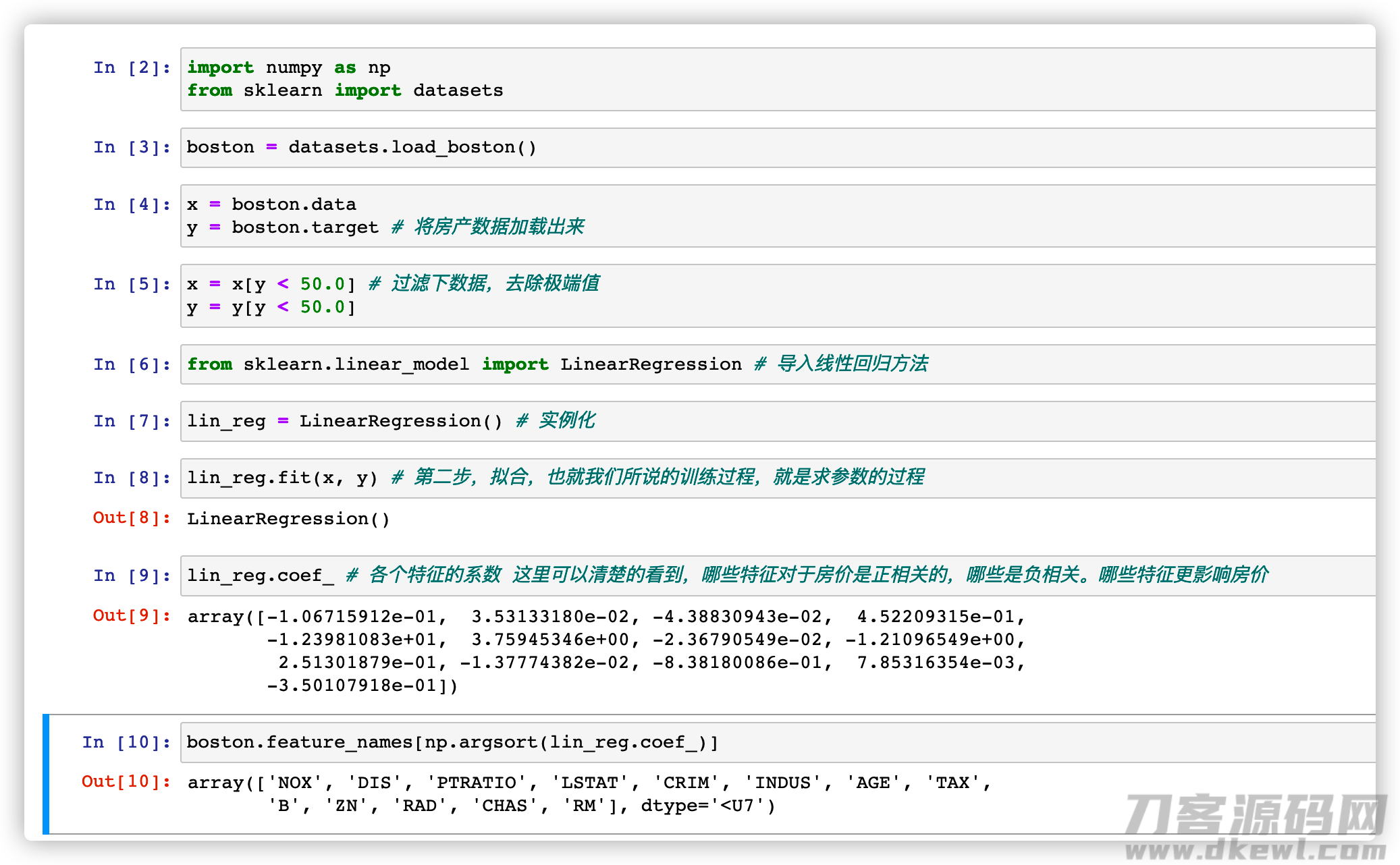
历经求得得到了（换句话说学习培训到）每个主要参数的值，随后假如地产开发商要想标价得话，能够搜集这种特点，随后应用实体模型的 predict 方式 能够得到一个房子价格的标准值。

随后大家还可以见到，哪些方面针对房子价格是成正比的，什么是成反比的。随后主要参数越大，越危害房子价格，这就是回归分析法针对結果的可实证性（有一些深度学习方式 是不兼容的）。

热烈欢迎关心凸凹试验室blog：aotu.io

或是关心凸凹试验室微信公众号（AOTULabs），不按时消息推送文章内容：