JITc语言编译器计算求余%上末地引起的一连串小故事

C1 RCE对%的解决

HotSpot VM的C1有一个RCE（Range Check Elimination，范畴查验清除）提升，说白了范畴查验清除，便是为了更好地恰当的抛出去数组越界出现异常，vm虚拟机必须在二维数组浏览的一些地区插进隐式的查验，可是这种查验会减少特性，例如在循环系统中每一次循环系统都得查验一次，因此HotSpot VM会想办法在很有可能的地区清除这种查验。我还在看C1 RCE的情况下发觉现阶段它对求余标记的适用比较欠缺，它只有解决形如下边的编码：

arr[x%arr.length] // 仅有除数是x.length的情况下，才可以运用RCE提升

假如余数是整数金额变量定义，它就不可以工作中了：

arr[x%3]
for(int i=0;i<10;i  ){
  arr[x]
}

事实上，依据JLS的界定，我们知道假如除数为整数金额变量定义（且等于零，由于0做为除数会抛出去运作时出现异常），是能够计算出結果的上末地的（也在于被除数的正负极），标准以下：

• x % -y ==> [0, y – 1]
• x % y ==> [0, y – 1]
• -x % y ==> [-y 1, 0]
• -x % -y ==> [-y 1, 0]

因此，我给JDK发过个patch，这个问题算作解决了。可是Nils提及，C2是不是有同样的提升呢？后边Tobias帮助确定了一下C2沒有，我再之后也进一步确定了，因此下一步是调查C2是不是能运用一样的提升。

调查为C2运用一样的提升

原本认为是较为trivial的事儿，为求余连接点的种类系统软件天赋加点编码，计算一下上末地就可以，事实上因为我那么做的，可是最终发觉那样沒有清除上末地。默认设置打开-XX: GenerateRangeChecks后，在二维数组浏览全过程中（Parse::array_addressing），C2依然转化成了范畴查验。

调节后发觉计算上末地压根沒有实行，由于C2建立完求余连接点后，会实行一个IGVN的全过程，即迭代更新的运用多种多样提升，在其中就包含理想，C2理想就是指运用许多 部分小提升的全过程，在这个事例中便是独特解决形如x%2^n,x%2^n-1和x%1的状况，假如除数是整数金额变量定义，它还会继续应用一个来源于https://book.douban.com/subject/1784887/书里边的优化算法，即Division by Invariant Integers using Multiplication(by Granlund and Montgomery)，搜过一下知乎问答有相近的文章内容，要想掌握关键点能够读一读https://zhuanlan.zhihu.com/p/151038723。知道缘故，因此我改了下编码，严禁了求余连接点的理想，想着这总就行了吧。

或是不好

是的，或是不好。虽然我已经严禁了对求余标记的理想提升，可是范畴查验或是转化成了。。。我又继续看编码，发觉除开理想的这一提升以外，C2在IR（正中间表明）结构的全过程中又 又 又 又 又对求余运算干了个提升！假如除数是整数变量定义，且是2^n，那麼C2会对它开展形变，IR如下图所示：

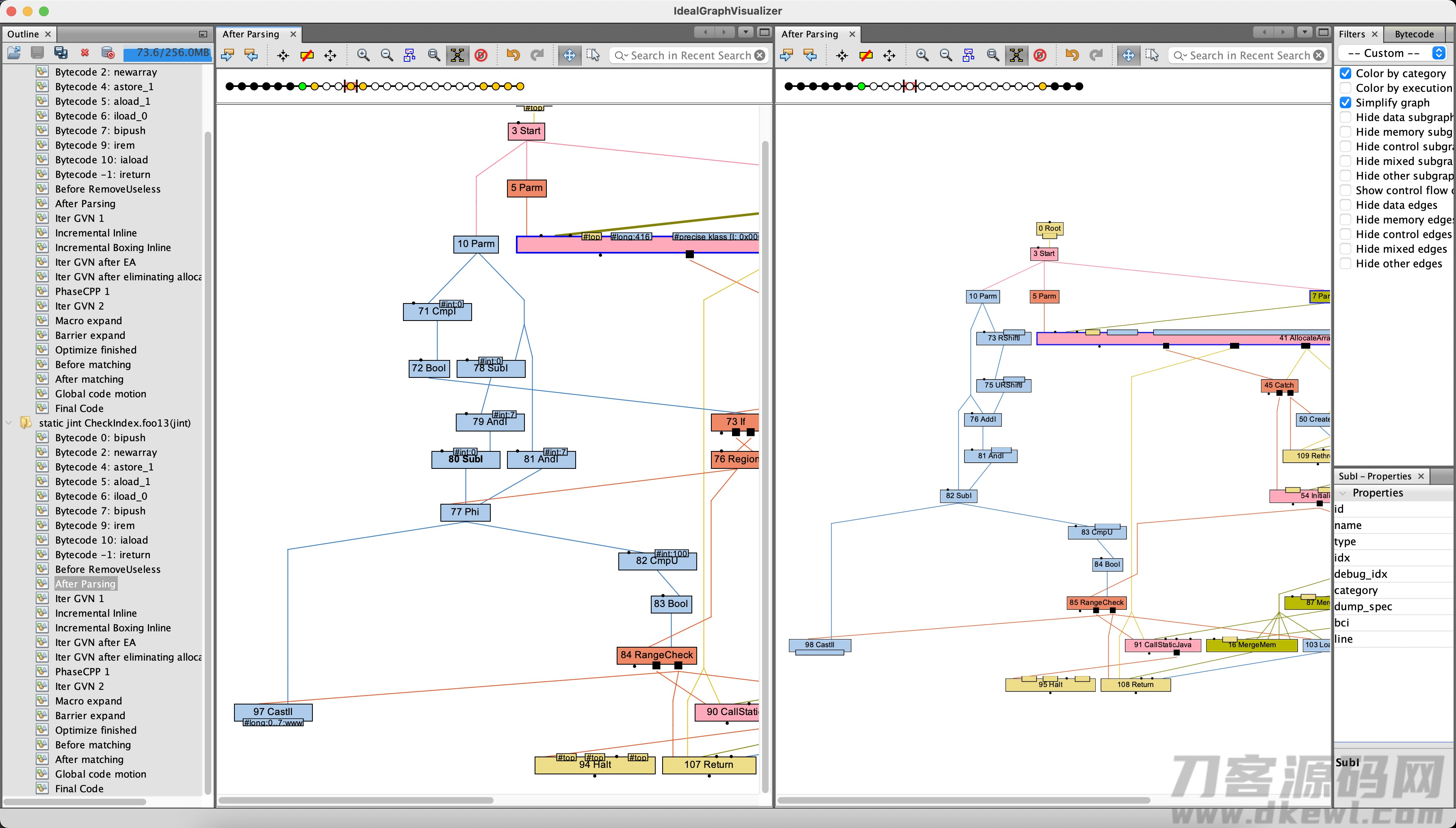
左侧的IR是 IR结构的情况下C2做的提升后的实际效果，右侧是理想提升后的实际效果。事实上他们做的事儿自身是较为反复的，并且历经检测发觉，理想提升的优化算法好些于IR结构全过程中的提升：

一个简易的micro benchmark：

public class ModPowerOf2 {
    @Benchmark
    public int testPositivePowerOf2() {
        int sum = 0;
        for (int i = 0; i < 1000; i  ) {
            sum  = i % 1;
            sum  = i % 2;
            sum  = i % 4;
            sum  = i % 8;
            sum  = i % 16;
            sum  = i % 32;
            sum  = i % 64;
            sum  = i % 128;
            sum  = i % 256;
            sum  = i % 512;
            sum  = i % 1024;
            sum  = i % 2048;
            sum  = i % 4096;
            sum  = i % 8192;
            sum  = i % 16384;
            sum  = i % 32768;
            sum  = i % 65536;
        }
        return sum;
    }

    @Benchmark
    public int testNegativePowerOf2() {
        int sum = 0;
        for (int i = 0; i < 1000; i  ) {
            sum  = i % -1;
            sum  = i % -2;
            sum  = i % -4;
            sum  = i % -8;
            sum  = i % -16;
            sum  = i % -32;
            sum  = i % -64;
            sum  = i % -128;
            sum  = i % -256;
            sum  = i % -512;
            sum  = i % -1024;
            sum  = i % -2048;
            sum  = i % -4096;
            sum  = i % -8192;
            sum  = i % -16384;
            sum  = i % -32768;
            sum  = i % -65536;
        }
        return sum;
    }
}

理想：

Benchmark Mode Cnt Score Error Units
ModPowerOf2.testNegativePowerOf2 avgt 25 8746.608 ± 139.777 ns/op
ModPowerOf2.testPositivePowerOf2 avgt 25 8735.545 ± 86.145 ns/op

IR结构提升：

Benchmark Mode Cnt Score Error Units
ModPowerOf2.testNegativePowerOf2 avgt 25 8693.797 ± 7.844 ns/op
ModPowerOf2.testPositivePowerOf2 avgt 25 6618.652 ± 1.739 ns/op

所以我提了个patch，提前准备清除IR结构做的提升来处理这个问题。

总结

我觉得为求余连接点计算上末地也是更有意义的，假如之后有别的提升会形变为求余运算，那麼他们能够运用这一计算，另外，为求余做统一健全的种类计算这件事情自身也是恰当的，因此我又提了个patch。能够见到，最后我只清除了C1 arr[x%4]的范畴查验，或是没能清除C2 arr[x%4]的范畴查验，是否之后可以说C1有的地区做的比C2好啦（狗头hh。