序言

我还在上一篇文章简易完成了在canvas移动矩形框（点线面），不清楚的小伙伴们可以看我本文：用canvas 完成矩形框的挪动（点、线、面）（1）。 ok,废话不多说，直接进入文章内容， 上一篇文章我留了许多难题，便是我还在画步移动我怎么知道我挪动的是哪一个种类，到底是点或是线或是面， 这就是这篇文章内容要处理的难题。 看完这篇能够 学得下边几个方面：

1. 分辨点与点中间的间距

2. 分辨点与平行线的关联（叉乘的应用）

3. canvas中如何画出正n边形。（转动）

其实我上边讲了这么多，实际上 便是为了更好地在2d图型做一个实际效果便是 snap ——吸咐，分辨当今点与当今蒙版上不规则图形的关联。

吸咐——完成点

阅读者你能思索下，假如想要你去做你能如何去做呢？ 假定蒙版上面有许多不规则图形，也有许多点。有些人讲了，哪一个挨近它不便是哪一个。ok 你答对了，实际上 便是去分辨当今点和蒙版上全部的点去核对，哪一个离的近，便是选定的哪一个点，这儿会牵涉到一个查看特性难题？ 有同学们便会问假如蒙版中有很多点呢？大家难道说就需要一个个去解析xml比较大小嘛，自然并不是这儿给大伙儿科谱一下一个空间几何数据库索引优化算法Rbush

RBush是一个性能卓越JavaScript库，用以点和矩形框的二维空间数据库索引。它根据提升的R树算法设计，适用批量插入。

我后边有时间会有大伙儿撸一遍Rbush的，这儿我得出参照连接 有兴趣爱好的同学们自主掌握下。这篇就无需Rbush，就用结合去储存数据信息了哈！ 这儿也有一点必须 注重的便是蒙版中的每一个点应当都每一个点都一个是案例，具备与众不同的id。 大家下面就再次更新改造下：

const current = 0;
const map = new Map();
constructor(x,y) {
    this.x = x || 0;
    this.y = y || 0;
    this.id =   current;
    map.set(this.id,[x,y]);
}
// 提升到Map上
add2Map() {
  pointMap.push(this)
  return this
}
//用于随机生成一个点
random(width,height){
    this.x = Math.random() * width;
    this.y = Math.random() * height;
    return this;
}
​
// 取平方根
abs() {
    return [Math.abs(this.x), Math.abs(this.y)]
}
​
//测算两个点中间的间距
distance(p) {
    const [x,y] = this.clone().sub(p).abs();
    return Math.sqrt(x*x   y * y);
}
​

我又再次写了一个画不规则图形的方式编码以下：

// 画不规则图形
function drawAnyPolygon(points) {
    if(!Array.isArray(points)) {
        return;
    }
    ctx.strokeStyle = 'black'
    ctx.setLineDash([]); 
    ctx.beginPath();
    const start = points[0];
    ctx.moveTo(start.x,start.y)
    points.slice(1).forEach(item => {
        ctx.lineTo(item.x,item.y)
    })
    ctx.closePath()
    ctx.stroke()
}

这一没有什么最重要的是什么，大家怎样依据一个点去转化成正多边形的点结合

CANVAS中如何画正多边形？

这儿大家看下不规则图形的界定：

正多边形就是指二维平面图内各边相同，各角也相同的不规则图形，也叫正多角形。

去较为电脑鼠标的点和蒙版中的点的间距了。大家首先看第一部分依据种类转化成点：

// 依据挪动的种类再次转化成点
function generatePointsByType(mousePoint,type = 'point',width = 200, height = 200) {
      const results = [];
      const { x, y } = mousePoint;
      const moveVec = end.clone().sub(start);
      const p1  =  new Point2d(x- width /2, y - height/2).add2Map();
      const p2 = new Point2d(x  width / 2, y - height/2).add2Map();
      const p3 = new Point2d(x  width / 2, y   height/2).add2Map();
      const p4 = new Point2d(x - width / 2, y   height/2).add2Map();
      return [p1,p2,p3,p4]
  }

这里有一点要留意的是便是p1,p2,p3,p4 达到的是顺时针方向，由于大家canvas绘图是以左上—–>左下方的。 这一点大伙儿在自身调节的要十分注意！！add2Map， 便是把点添加到Map中。我还在上边填补上。我得出下一部分编码：较为电脑鼠标的点和蒙版中的点中间的尺寸。

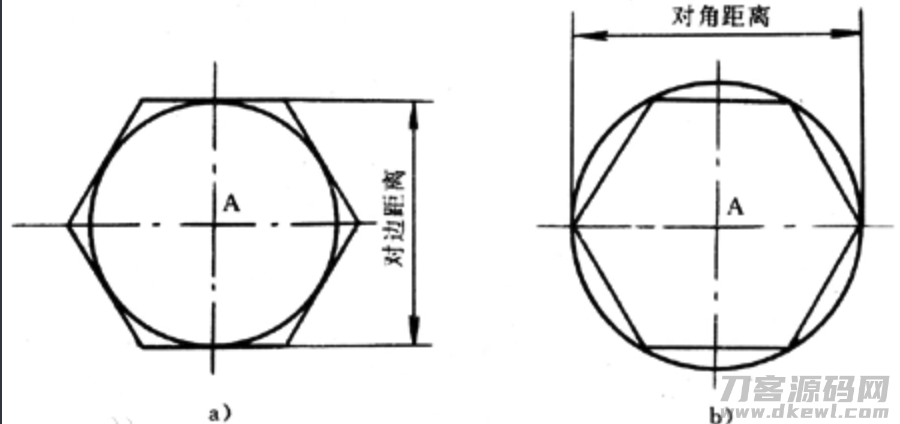
从图上我们可以获得： 正多形的产生 只不过便是二种

1. 以当今点为圆心点、绘制一个外接圆、之后呢 依据边数开展等分

2. 以当今点为圆心点、绘制一个内接圆、之后呢 依据边数开展等分

基本原理大家知道，运用到大家canvas如何去完成呢？ 实际上 也非常简单，大家以圆心点和圆上的一点，做为起止的空间向量。随后不断转动 2π/n 的视角 就可以获得全部的点了。 拥有点大家就可以绘制正多边形了。 这儿是外接圆算不规则图形的构思，对于内接圆如何去算， 给大伙儿一个课后练习思考题