摘要
SMO优化算法是SVM优化算法的关键,下面我们来看看SMO优化算法的全过程。在这个过程中,我们需要定义一些辅助函数,比如选择第二个自变量的函数。让我们一起来感受一下吧!
正文
前边早已对感知机和SVM开展了简略的简述,这节是SVM优化算法的完成全过程用以輔助了解SVM优化算法的主要内容,随后依靠sklearn对SVM工具箱开展完成。
SVM优化算法的关键是SMO优化算法的完成,最先对SMO优化算法全过程开展完成,先向一些輔助涵数开展界定:
1 # 先界定一些輔助涵数 2 # 选择第二自变量涵数 3 def select_J_rand(i, m): 4 j=i 5 while(j==i): 6 j = int(random.uniform(0, m)) 7 return j 8 9 # 界定对α开展剪裁的涵数 10 def clip_alpha(aj, H, L): 11 if aj > H: 12 aj=H 13 if L > aj: 14 aj = L 15 return aj
随后完成一个简易版的SMO优化算法:
"""
Input:dataX, dataY, C(处罚因素), toler(承受度), iter_num
Output: alpha、b
"""
def smo_simple(dataX, dataY, C, toler, iter_num): dataMatrix = mat(dataX); labelMat = dataY.transpose() # 复位主要参数 b = 0; m, n = np.shape(dataMatrix) alphas = mat(np.zeros((m, 1))) iter = 0 # 当超出迭代更新频次终止 while iter < iter_num: # 纪录α1和α2转变频次 alphaPairsChanged = 0 for i in range(m): # 测算f(xi),预测分析类型 fXi = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) b # 数据误差 Ei = fXi - float(labelMat[i]) # 当不符合条件时,选择自变量j,这儿要分辨α是不是在[0,C]内,若超出则不会再开展提升 if ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and alphas[i] > 0): j = select_J_rand(i, m) # 测算x2的估计值y2 fXj = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) b Ej = fXj - float(labelMat[j]) alpha_I_old = alphas[i].copy() alpha_J_old = alphas[j].copy() if (labelMat[i] != labelMat[j]): L = max(0, alphas[j] - alphas[i]) H = min(C, C alphas[j] - alphas[i]) else: L = max(0, alphas[i] alphas[j] - C) H = min(C, alphas[i] alphas[j]) if L == H: print("L == H") continue eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] * dataMatrix[i, :].T - dataMatrix[j, :] * dataMatrix[j, :].T if eta > 0: print("eta > 0") continue alphas[j] -= labelMat[j] * (Ej - Ei)/eta alphas[j] = clip_alpha(alphas[j], H, L) # 当α2不会再转变 if (abs(alphas[j]-alpha_J_old) < 0.00001): print("j not moving enough") continue # 升级α1 alphas[i] = labelMat[i] * labelMat[j] * (alpha_J_old - alphas[j]) # 测算b1和b2 b1 = b - Ei - labelMat[i] * (alphas[i] - alpha_I_old) * dataMatrix[i, :] * dataMatrix[i, :].T - labelMat[j] * (alphas[j] - alpha_J_old) * dataMatrix[i, :] * dataMatrix[j, :].T b2 = b - Ej - labelMat[i] * (alphas[i] - alpha_I_old) * dataMatrix[i, :] * dataMatrix[j, :].T - labelMat[j] * (alphas[j] - alpha_J_old) * dataMatrix[j, :] * dataMatrix[j, :].T if (alphas[i] > 0) and (alphas[i] < C): b = b1 elif (alphas[j] > 0) and (alphas[j] < C): b = b2 else: b = (b1 b2)/2 alphaPairsChanged = 1 if alphaPairsChanged == 0: iter = 1 else: iter = 0 print("iteration number: %d"%iter) return b, alphas
SMO优化算法具备一定的偶然性,因而每一次运作的結果不一定同样。上边便是一个简易的SMO优化算法的完成一部分,针对小批量生产数据信息能够满足需求,但当信息量过度巨大时,上边的优化算法的高效率可能比较慢,这是由于在α的选择问题上,下边给予一种改善的SMO优化算法,改善的SMO优化算法会根据一个外循环挑选第一个α的值,挑选方式 是在解析xml全部样版(数据)和非界限α中开展扫描仪,说白了非界限α就是指这些并不等于0或是C的α值,创建这种α值的目录,在目录中开展解析xml,并在扫描仪时绕过不会再更改的α开展解析xml。下边是实际完成全过程
最先界定輔助涵数用以储存和升级E,并创建一个算法设计储存自变量
1 # 最先创建3个輔助涵数用以对E开展缓存文件,及其1种用以储存数据信息的算法设计 2 # 储存自变量的算法设计 3 class optStruct: 4 def ._init._(self, dataX, dataY, C, toler): 5 self.X = dataX 6 self.Y = dataY 7 self.C = C 8 self.toler = toler 9 self.m = np.shape(dataX)[0] 10 self.alphas = np.mat(zeros((self.m, 1))) 11 self.b = 0 12 # cache第一列入实效性标志位,第二列入E值 13 self.eCache = np.mat(np.zeros((self.m, 2))) 14 15 # 测算E值并回到,因为经常应用独立写出一个涵数 16 def calcEk(oS, k): 17 fXk = float(np.multiply(oS.alphas, oS.labelMat).T * (oS.X * oS.X[k, :].T)) oS.b 18 Ek = fXk - float(oS.labelMat[k]) 19 return Ek 20 21 # 用以挑选第二个α的值,确保每一次提升选用较大的步幅 22 def select_J(i, oS, Ei): 23 maxK = -1; maxDeltaE = 0; Ej = 0 24 oS.eCache[i] = [1, Ei] 25 validEcacheList = nonzero(oS.eCache[:, 0].A)[0] 26 if len(validEcacheList) > 1: 27 for k in validEcacheList: 28 if k == i: 29 continue 30 Ek = calcEk(oS, k) 31 deltaE = abs(Ei - Ek) 32 # 挑选转变较大的那一个 33 if deltaE > maxDeltaE: 34 maxK = k 35 maxDeltaE = deltaE 36 Ej = Ek 37 return maxK, Ej 38 else: 39 j = select_J_rand(i, oS.m) 40 Ej = calcEk(oS, j) 41 return j, Ej 42 43 44 def updateEk(oS, k): 45 Ek = calcEk(oS, k) 46 oS.eCache[k] = [1, Ek]
下面便是SMO优化算法的改善版本号
1 # 与simpleSMO一致,升级的alpha存进cache中 2 def innerL(i, oS): 3 Ei = calcEk(oS, i) 4 if ((oS.labelMat[i] * Ei < -oS.toler) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.toler) and (oS.alphas[i] > 0)): 5 j, Ej = select_J(i, oS, Ei) 6 alpha_I_old = oS.alphas[i].copy() 7 alpha_J_old = oS.alphas[j].copy() 8 if oS.labelMat[i] != oS.labelMat[j]: 9 L = max(0, oS.alphas[j] - oS.alphas[i]) 10 H = min(oS.C, oS.C oS.alphas[j] - oS.alphas[i]) 11 else: 12 L = min(0, oS.alphas[i] oS.alphas[j] - oS.C) 13 H = max(oS.C, oS.alphas[i] oS.alphas[j]) 14 if H == L: 15 return 0 16 eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].T 17 if eta >= 0: 18 return 0 19 oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej)/eta 20 oS.alphas[j] = clip_alpha(oS.alphas[j], H, L) 21 updateEk(oS, j) 22 if abs(oS.alphas[j] - alpha_J_old) < 0.00001: 23 return 0 24 oS.alphas[i] -= oS.labelMat[i] * oS.labelMat[j] * (oS.alphas[j] - alpha_J_old) 25 updateEk(oS, i) 26 b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alpha_I_old) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * (oS.alphas[j] - alpha_J_old) * oS.X[i, :] * oS.X[j, :].T 27 b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alpha_I_old) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * (oS.alphas[j] - alpha_J_old) * oS.X[j, :] * oS.X[j, :].T 28 if oS.alphas[i] > 0 and oS.alphas[i] < oS.C: 29 oS.b = b1 30 elif oS.alphas[j] > 0 and oS.alphas[j] < oS.C: 31 oS.b = b2 32 else: 33 os.b = (b1 b2)/2 34 return 1 35 else: 36 return 0 37 38 39 def smoP(dataX, labelMat, C, toler, maxIter, kTup=('lin', 0)): 40 oS = optStruct(mat(dataX), mat(labelMat).transpose(), C, toler) 41 iter = 0 42 entireSet = True 43 alphaPairsChanged = 0 44 while (iter < maxIter) and alphaPairsChanged > 0 or entireSet: 45 alphaPairsChanged = 0
# 检索第一个自变量的值,选用2个方式 更替开展的方法,运用entireSet自变量操纵 46 # 第一种解析xml全体人员样版 47 if entireSet: 48 for i in range(oS.m): 49 alphaPairsChanged = innerL(i, oS) 50 iter = 1 51 # 第二种解析xml非界限样版 52 else: 53 nonBoundIs = nonzero((oS.alphas.A > 0) * oS.alphas.A < C)[0] 54 for i in nonBoundIs: 55 alphaPairsChanged = innerL(i, oS) 56 iter = 1 57 if entireSet: 58 entireSet = False 59 elif alphaPairsChanged == 0: 60 entireSet = True 61 return oS.alphas, oS.b
获得到α的值后,则能够进一步求出实体模型的w和b,实际完成全过程为:
1 def calW(alphas, dataArr, classLabels): 2 X = mat(dataArr) 3 labelMat = mat(classLabels).transpose() 4 m, n = shape(X) 5 w = zeros((m, 1)) 6 for i in range(m): 7 w = multiply(alphas[i] * labelMat[i], X[i, :]) 8 return w
以上即是SVM的完成全过程,是对线形分为的数据信息的归类的完成全过程,当针对离散系统数据信息,必须应用到核函数,在完成全过程中也比较简单,只需只需将(xi·xj)更换为核函数就可以,实际完成全过程以下
1 # 最先原来的算法设计时要测算核引流矩阵,将以下编码添加算法设计编码一部分就可以 2 self.K = mat(zeros(self.m, self.m)) 3 for i in range(self.m): 4 self.K[:, i] = kernelTrans(self.X, self.X[i, :], self.kTup)
下面完成核变换涵数
1 def kernelTrans(X, A, kTup): 2 m, n = shape(X) 3 K = mat(zeros((m, 1))) 4 if kTup['0'] == 'lin': 5 K = X * A.T 6 elif kTup[0] == 'rbf': 7 for j in range(m): 8 deltaRow = X[j, :] - A 9 K[j] = deltaRow * deltaRow.T 10 K = exp(K/(-1 * kTup[1] ** 2)) 11 else: 12 raise NameError('沒有界定核函数') 13 return K
随后必须在主要参数测算的涵数里将相匹配的xi*xj更换为核函数就可以:
1 # 最先是innerL中 2 eta = 2.0 * oS.K[i, j] - oS.K[i, i] - oS.K[j, j] 3 b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alpha_I_old) * oS.K[i, i] - oS.labelMat[j] * (oS.alphas[j] - alpha_J_old) * oS.K[i, j] 4 b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alpha_I_old) * oS.K[i, j] - oS.labelMat[j] * (oS.alphas[j] - alpha_J_old) * oS.K[j, j] 5 6 # 随后是calcEk 7 fXk = float(multiply(oS.alphas, oS.labelMat).T * oS.K[:, k] oS.b)
到此,SVM优化算法的完成全过程基本上早已完成了,下面大家运用MNIST的数据,对手写数字开展归类和识别,MNIST笔写识别数据信息在网络上就可以寻找。
最先必须写一个获取数据的涵数及其将函数图像转换为引流矩阵的涵数:
1 def img2Vector(filename): 2 returnVec = zeros((1, 1024)) 3 fr = open(filename) 4 for i in range(32): 5 lineStr = fr.readline() 6 for j in range(32): 7 returnVec[0, 32*i j] = int(lineStr[j]) 8 return returnVec
1 def loadImages(dir): 2 hwLabels = [] 3 trainingFileList = os.listdir(dir) 4 m = len(trainingFileList) 5 for i in range(m): 6 fileNameStr = trainingFileList[i] 7 fileStr = fileNameStr.split('.')[0] 8 classNumStr = int(fileStr.split('_')[0])
# 只考虑到二分类难题 9 if classNumStr == 9: 10 hwLabels.append(-1) 11 else: 12 hwLabels.append(1) 13 trainingMat[i, :] = img2Vector('%s/%s' % (dir, fileNameStr)) 14 return trainingMat, hwLabels
随后撰写源程序,用以归类和检测。
1 def testDigits(kTup=('rbf', 10)):
# 读取数据 2 dataArr, labelArr = loadImages('trainingDigits')
# 运用SMO优化算法求得出α和b 3 alphas, b = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup) 4 dataMat = mat(dataArr) 5 labelMat = mat(labelArr).transpose()
# 获得适用空间向量的数据库索引 6 svInd = nonzero(alphas.A > 0)[0]
# 获得适用空间向量 7 svs = dataMat[svInd] 8 labelSv = labelMat[svInd] 9 m, n = shape(dataMat) 10 errorCount = 0 11 for i in range(m): 12 kernelEval = kernelTrans(svs, dataMat[i, :], kTup) 13 predict = kernelEval.T * multiply(labelSv, alphas[svInd]) b 14 if sign(predict) != sign(labelArr[i]): 15 errorCount = 1 16 print('there are %d Support Vectors'%shape(svs)[0]) 17 print('the error rate is %f' % (errorCount / (len(labelMat)))) 18 test_dataArr, test_labelArr = loadImages('testDigits') 19 test_dataMat = mat(test_dataArr) 20 test_labelMat = mat(test_labelArr).transpose() 21 m1, n1 = shape(test_dataMat) 22 test_errorCount = 0 23 for i in range(m1): 24 kernelEval = kernelTrans(svs, test_dataMat[i, :], kTup) 25 predict = kernelEval.T * multiply(labelSv, alphas[svInd]) b 26 if sign(predict) != sign(test_labelArr[i]): 27 errorCount = 1 28 print('the error rate is %f' % (test_errorCount / (len(test_labelMat))))
輸出結果以下:

到此,以上是一个详细的SVM优化算法用以二分类的完成全过程,核函数能够开展改动和更换,与此同时,针对多归类状况等同于创建好几个支持向量机开展归类,全过程这儿不会再过多阐释,下面,应用python中sklearn包对Mnist的数据归类完成一遍。
最先是以sklearn导进svm包,并获取数据
1 from sklearn import svm 2 train_dataArr, train_labelArr = loadImages(dir)
随后是实体模型的复位,这儿实体模型中有一些主要参数,其实际表明以下
1 model = svm.SVC(C=200, kernel='rbf', tol=1e-4, max_iter=-1, degree=3, gamma='auto_deprecated', coef0=0, shrinking=True, 2 probability=False, cache_size=200, verbose=False, class_weight=None, decision_function_shape='ovr') 3 """ 4 C: 处罚因素,默认设置为1.0,C越大,等同于处罚松弛变量,期待松弛变量贴近0,即对误归类的处罚扩大,趋于对训练集全分对的状况,那样对训练集检测时准确度很高,但泛化能力弱。C值小,对误归类的处罚减少,容许容错机制,将她们当做噪音点,泛化能力较强。 5 tol: 承受度阀值 6 max_iter: 迭代更新频次 7 kernel:核函数,包含: 8 linear(线形核):u*v 9 poly(代数式核):(gamma * u * v coef0)^degree 10 rbf(高斯核): exp(-gamma|u-v|^2) 11 sigmoid核: tanh(gamma*u*v coef0) 12 degree: 代数式核中的层面 13 gamma: 核函数中的主要参数,默认设置为“auto”,挑选1/n_features 14 coef: 代数式核和simoid核中的常数项,仅对这两个核函数合理 15 probability: 是不是选用几率可能,默认设置为False 16 shrinking: 是不是选用shrinking heuristic方式 ,默认设置为true 17 cache_size: 核函数的缓存文件尺寸,默认设置为200 18 verbose: 是不是容许沉余輸出 19 class_weight: 类型权重值 20 decision_function_shape: 能够取'ovo'一对一和'ovr'一对别的 21 """
随后便是数据信息开展训炼,并查询训炼准确度
1 model.fit(mat(train_dataArr), mat(train_labelArr).transpose()) 2 train_score = model.score(mat(train_dataArr), mat(train_labelArr).transpose()) 3 print('训练集上的准确度为%s'%train_score) 4 5 test_dataArr, test_labelArr = loadImages('E:\材料\PythonML_Code\Charpter 5\data\\testDigits'.format(dir)) 6 test_score = model.score(mat(test_dataArr), mat(test_labelArr).transpose()) 7 print('检测集在的准确度为%f' % test_score)
最后結果为:
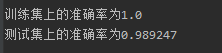
到此,SVM的基本上內容已基本上结束,除此之外也有运用SVM开展回归分析的优化算法及其选用SVM优化算法开展半监督学习的优化算法,后边见到这一块会进一步健全这一块內容。
关注不迷路
扫码下方二维码,关注宇凡盒子公众号,免费获取最新技术内幕!






评论0